Abstract

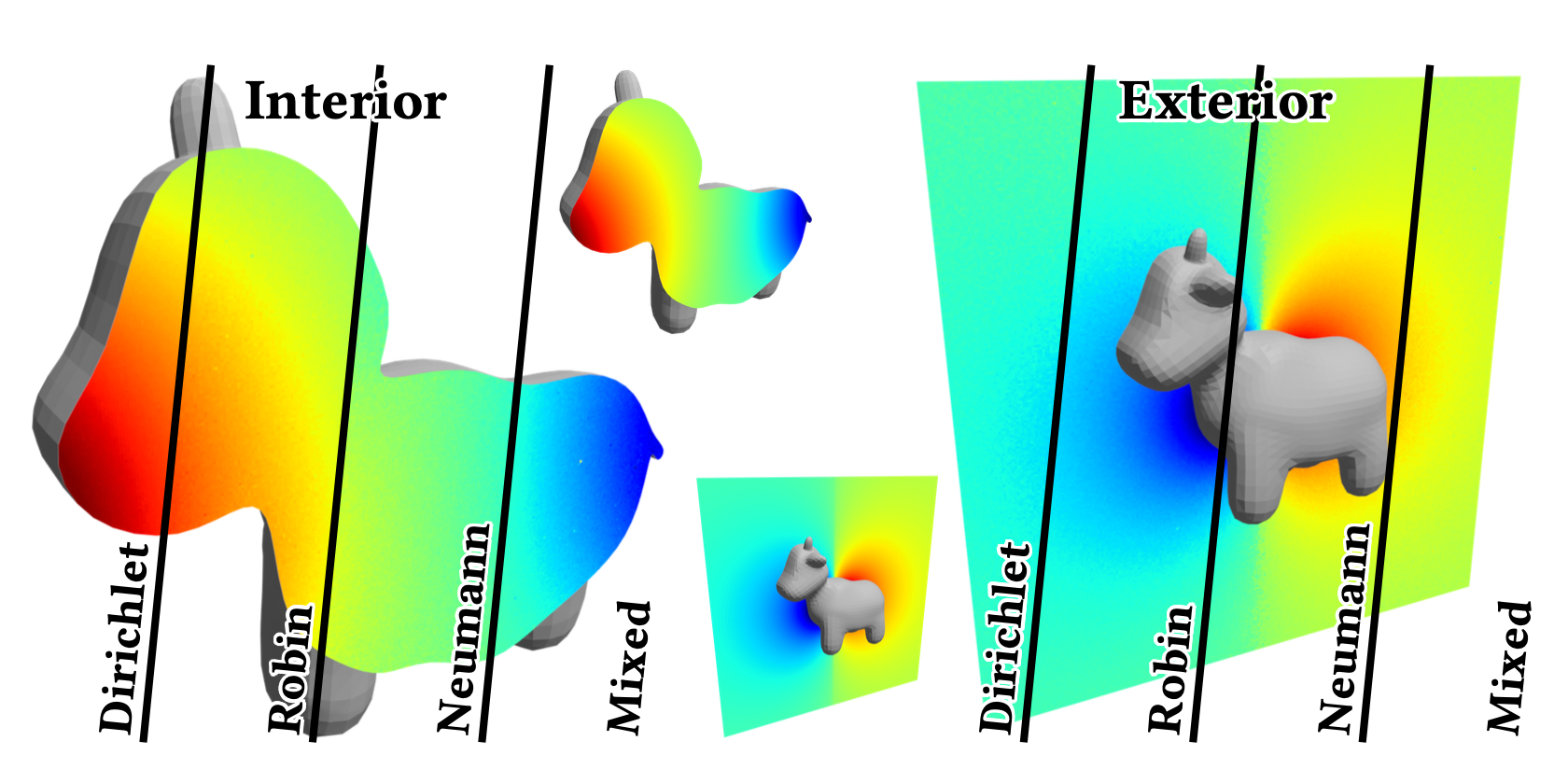
We introduce the walk-on-boundary (WoB) method for solving boundary value problems to computer graphics. WoB is a grid-free Monte Carlo solver for certain classes of second order partial differential equations. A similar Monte Carlo solver, the walk-on-spheres (WoS) method, has been recently popularized in computer graphics due to its advantages over traditional spatial discretization-based alternatives. We show that WoB's intrinsic properties yield further advantages beyond those of WoS. Unlike WoS, WoB naturally supports various boundary conditions (Dirichlet, Neumann, Robin, and mixed) for both interior and exterior domains. WoB builds upon boundary integral formulations, and it is mathematically more similar to light transport simulation in rendering than the random walk formulation of WoS. This similarity between WoB and rendering allows us to implement WoB on top of Monte Carlo ray tracing, and to incorporate advanced rendering techniques (e.g., bidirectional estimators with multiple importance sampling, the virtual point lights method, and Markov chain Monte Carlo) into WoB. WoB does not suffer from the intrinsic bias of WoS near the boundary and can estimate solutions precisely on the boundary. Our numerical results highlight the advantages of WoB over WoS as an attractive alternative to solve boundary value problems based on Monte Carlo.

Video

• A recording of a 12-minute talk is on YouTube.
• A recording of a 30-minute talk about this work presented at CSIG SIGGRAPH Webinar Series is avaialble here (KouShare).

Additional Note

• The applications of the direct BIE (Eq. 6) to exterior domain problems typically uses the form we get by setting c(x) = 0 in Eq. 6, but we have a different form in Table 1. We can find this form of equation for exterior domain problems in Section 3.5 of the book by H. Power and L.C. Wrobel titled "Boundary Integral Methods in Fluid Mechanics" (1995), for example.
• The decay rates outlined in Section 4.5.1 are for problems in 3D or higher dimensions. For 2D problems, the decay rates are outlined in Section 3.5 of the book above, for example.

Publication

@article{Sugimoto:2023:WoB,
    title = {A Practical Walk-on-Boundary Method for Boundary Value Problems},
    author = {Sugimoto, Ryusuke and Chen, Terry and Jiang, Yiti and Batty, Christopher and Hachisuka, Toshiya},
    title = {A Practical Walk-on-Boundary Method for Boundary Value Problems},
    year = {2023},
    publisher = {Association for Computing Machinery},
    address = {New York, NY, USA},
    volume = {42},
    number = {4},
    doi = {10.1145/3592109},
    journal = {ACM Trans. Graph.},
    month = {jul},
    articleno = {81},
    numpages = {16}
}